DEF BLOG :

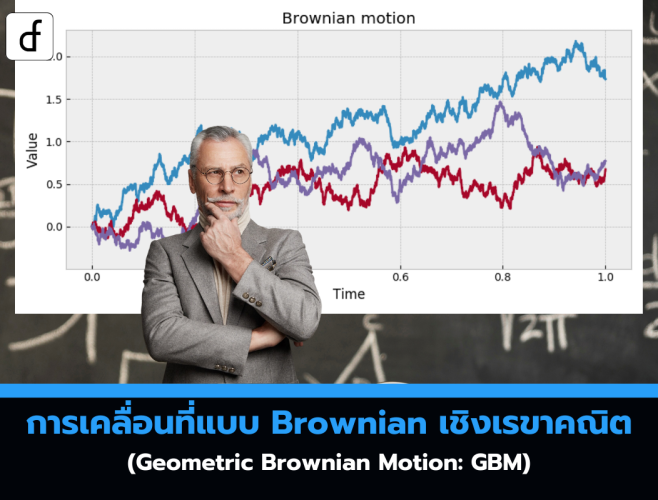
Geometric Brownian Motion (GBM) เป็นแบบจำลองพื้นฐานที่ใช้กันอย่างแพร่หลายในการอธิบายพฤติกรรมของราคาสินทรัพย์ในช่วงเวลา โดยโมเดลนี้รับประกันว่าราคาจะไม

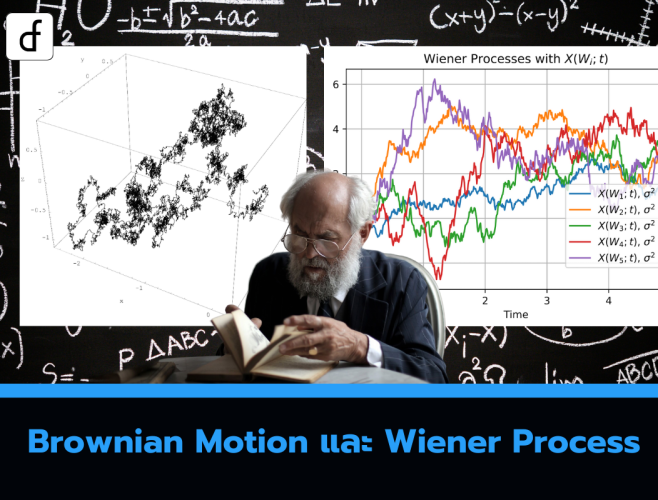
ก่อนหน้านี้เราได้แนะนำ Brownian Motion และ Wiener Process เพื่อเป็นรากฐานของการสร้างแบบจำลองเส้นทางราคาสินทรัพย์ อย่างไรก็ตาม Brownian Motion แบบปกติม

ในบทความนี้ เราจะนิยาม Brownian Motion และอธิบายคุณสมบัติบางอย่าง ซึ่งมีความสำคัญมากในการสร้างโมเดลเส้นทางราคาสินทรัพย์ในอนาคต ก่อนหน้านี้เราได้แนะนำแ

ปัจจุบัน Python ได้กลายเป็นภาษาหลักในวงการการเงินเชิงปริมาณ (quant finance) ใช้งานอย่างแพร่หลายในทั้งธนาคารเพื่อการลงทุน (investment banks) และกองทุนเ

ในบทความก่อนหน้า เราได้แนะนำหนังสือ C++ หลายเล่มเพื่อช่วยเรียนรู้ไวยากรณ์ (syntax) ที่จำเป็นสำหรับการสร้างโมเดลการกำหนดราคาผลิตภัณฑ์อนุพันธ์ (derivati

การเรียนรู้วิธีการนำแบบจำลองมาประยุกต์ใช้จำเป็นต้องมีความเข้าใจในทฤษฎีที่ลึกซึ้ง ซึ่งจะช่วยให้สามารถใช้กลยุทธ์ทางคณิตศาสตร์ที่จำเป็นในการเพิ่มประสิทธิ

โพสต์นี้เป็นส่วนหนึ่งของชุดรายการหนังสือสำหรับนักวิเคราะห์เชิงปริมาณ (quantitative analysts) มือใหม่ บทความอื่น ๆ ในชุดนี้จะเน้นไปที่การเขียนโปรแกรม C

แนวคิดหลักสองประการในด้านการเงินเชิงปริมาณ (quantitative finance) คือสมบัติมาร์คอฟ (Markov property) และสมบัติมาร์ติงเกล (Martingale property) โดยสมบั

แคลคูลัสเชิงสุ่ม (Stochastic calculus) ถูกใช้อย่างแพร่หลายในวงการการเงินเชิงปริมาณ (quantitative finance) เพื่อสร้างแบบจำลองราคาสินทรัพย์แบบสุ่ม (rand