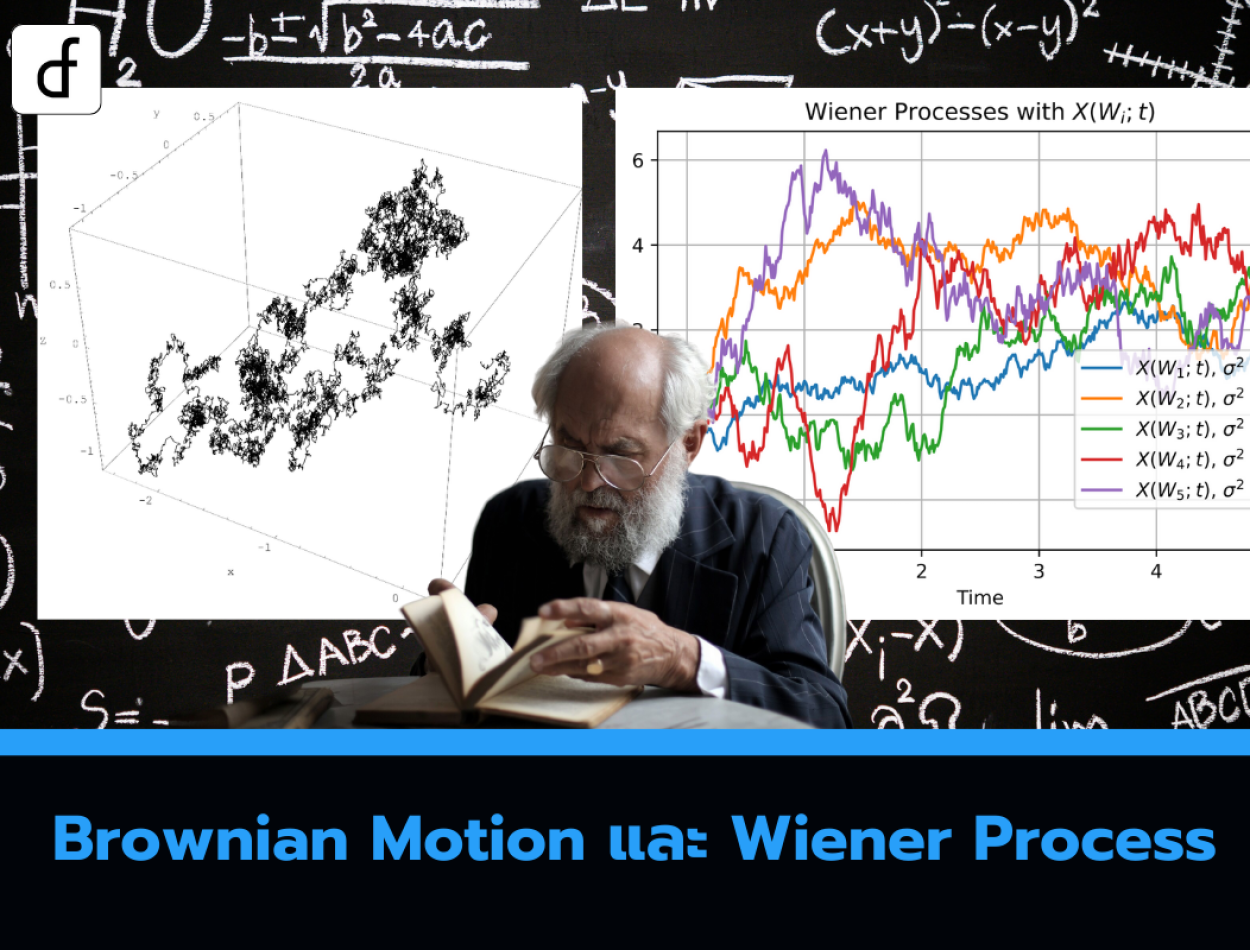
Brownian Motion และ Wiener Process

ในบทความก่อนหน้านี้บนเว็บไซต์ เราได้แนะนำแคลคูลัสเชิงสุ่ม (stochastic calculus) ในบริบทของบทบาทที่มีต่อการเงินเชิงปริมาณ (quantitative finance) โดยคุณสมบัติของ Markov และ Martingale ก็ได้ถูกนิยามไว้เพื่อเตรียมพร้อมสำหรับเครื่องมือทางคณิตศาสตร์ที่จำเป็นในการจำลองเส้นทางราคาสินทรัพย์

ในทั้งสองบทความนี้ ได้มีการกล่าวว่า Brownian motion จะใช้เป็นแบบจำลองสำหรับเส้นทางราคาสินทรัพย์เมื่อเวลาผ่านไป ในบทความนี้ Brownian motion จะได้รับการนิยามอย่างเป็นทางการ และจะอธิบายอนุพันธ์ทางคณิตศาสตร์ของมันซึ่งก็คือ Wiener process จะมีการแสดงให้เห็นว่า standard Brownian motion นั้นไม่เพียงพอสำหรับการจำลองความเคลื่อนไหวของราคาสินทรัพย์ และ geometric Brownian motion เป็นสิ่งที่เหมาะสมมากกว่า

จากการอภิปรายก่อนหน้านี้เกี่ยวกับคุณสมบัติของ Markov และ Martingale ได้มีการทดลองโยนเหรียญแบบไม่ต่อเนื่อง โดยใช้จำนวนช่วงเวลาที่กำหนดไว้แบบ (arbitrary) เป้าหมายในที่นี้คือ การมุ่งไปสู่การเดินสุ่มแบบเวลาต่อเนื่อง (continuous-time random walk) ซึ่งจะเป็นแบบจำลองที่ซับซ้อนยิ่งขึ้นสำหรับราคาสินทรัพย์ที่เปลี่ยนแปลงตามเวลา เพื่อให้บรรลุเป้าหมายนี้ จำเป็นต้องเพิ่มจำนวนช่วงเวลา (time steps) อย่างไรก็ตาม วิธีการเพิ่มจะต้องดำเนินไปในลักษณะเฉพาะ เพื่อหลีกเลี่ยงผลลัพธ์ที่ไร้ความหมาย (เช่น อินฟินิตี้)

พิจารณาช่วงเวลาแบบต่อเนื่องที่เป็นจำนวนจริง [0,T], โดยที่ T > 0 ในช่วงเวลานี้จะมีการโยนเหรียญ N ครั้ง โดยแต่ละครั้งใช้เวลา T/N ดังนั้นการโยนเหรียญจะเกิดขึ้นอย่างสม่ำเสมอในเชิงเวลา พร้อมกันนี้จะมีการปรับค่าผลตอบแทนที่ได้จากการโยนแต่ละครั้ง ลำดับของตัวแปรสุ่มไม่ต่อเนื่อง (discrete random variables) ที่แทนการโยนเหรียญคือ Zi∈{−1,1}. นอกจากนี้ยังสามารถนิยามลำดับของตัวแปรสุ่มไม่ต่อเนื่องอีกลำดับหนึ่งได้คือ

${\widetilde{\mathrm{ Z}}}_i\in \{\sqrt{T/N},-\sqrt{T/N}\}$

การนิยามลำดับของตัวแปรสุ่มนี้มีเป้าหมายเพื่อให้ได้ค่าการเปลี่ยนแปลงกำลังสองเฉพาะเจาะจง (quadratic variation) ของการโยนเหรียญ

ค่าการเปลี่ยนแปลงกำลังสอง (quadratic variation) ของลำดับ DRVs นิยามเป็นผลรวมของผลต่างยกกำลังสองระหว่างค่าปัจจุบันและค่าก่อนหน้า:

$$\begin{array}{r}\sum _{k=1}^i{(S_k-S_{k-1})}^2\end{array}$$

สำหรับ  ซึ่งเป็นลำดับตัวแปรสุ่มการโยนเหรียญชุดแรก ค่าการเปลี่ยนแปลงกำลังสองคือ:

$$\begin{array}{r}\sum _{k=1}^i{(S_k-S_{k-1})}^2=i\end{array}$$

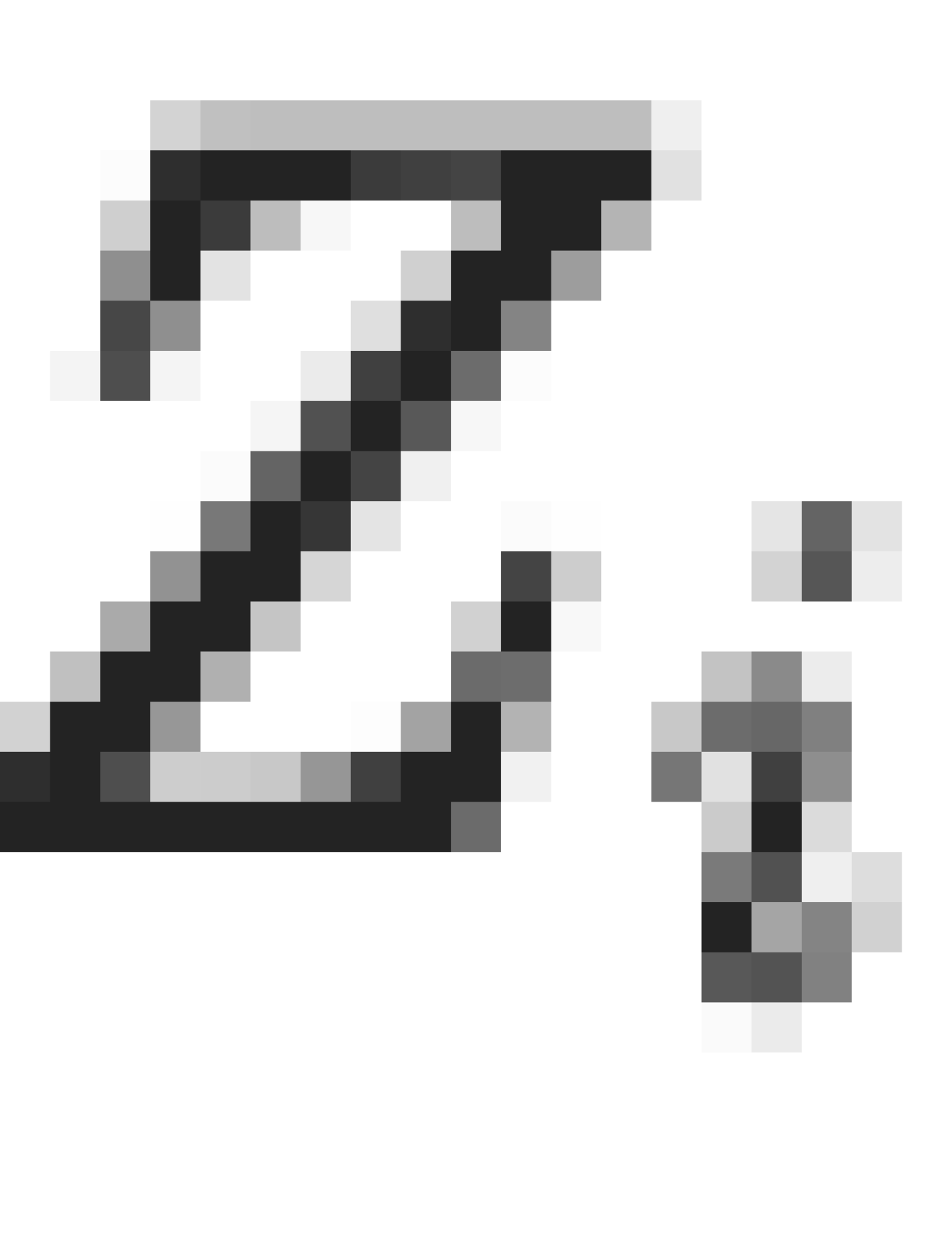
สำหรับ 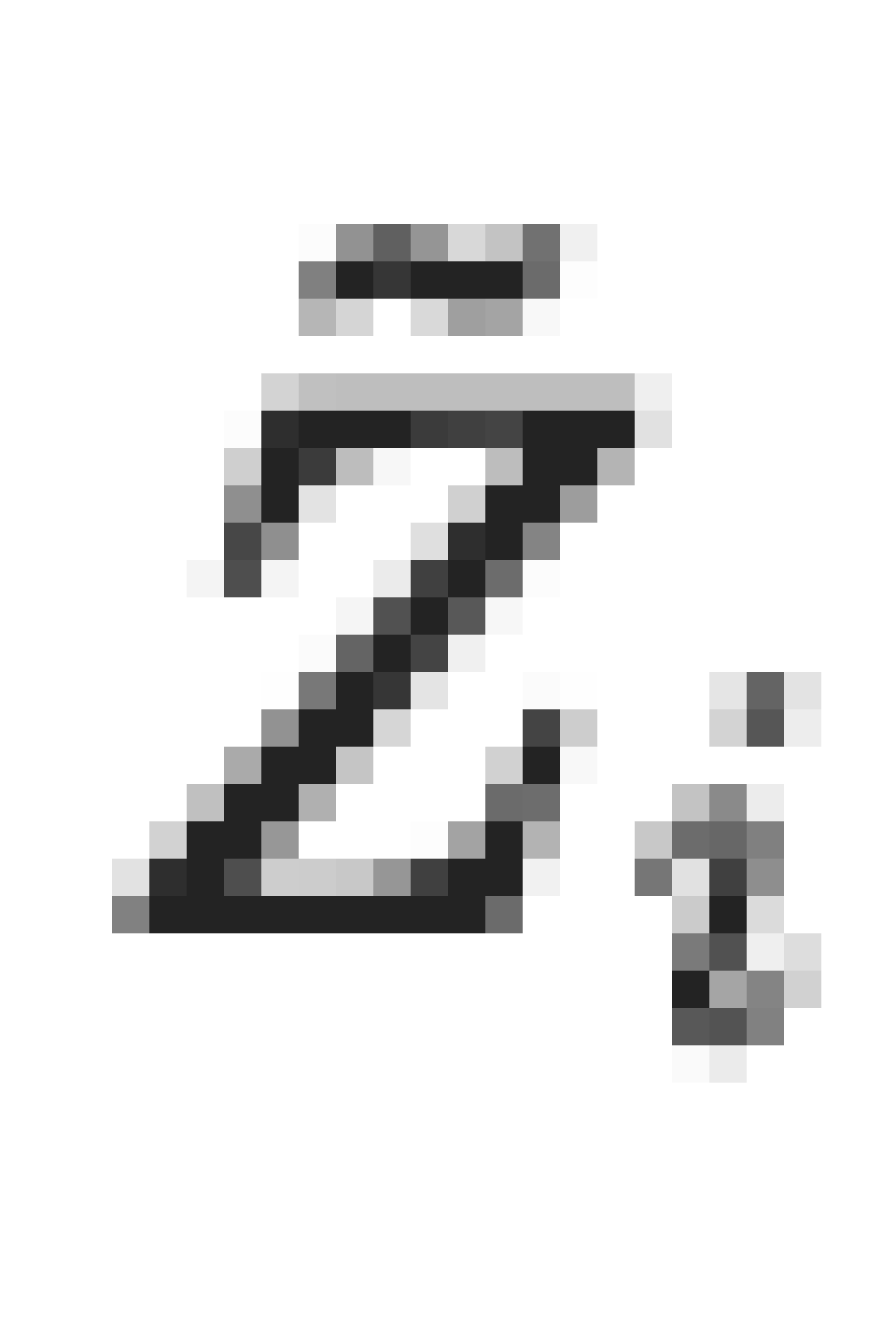 ค่าการเปลี่ยนแปลงกำลังสองของผลรวมย่อย  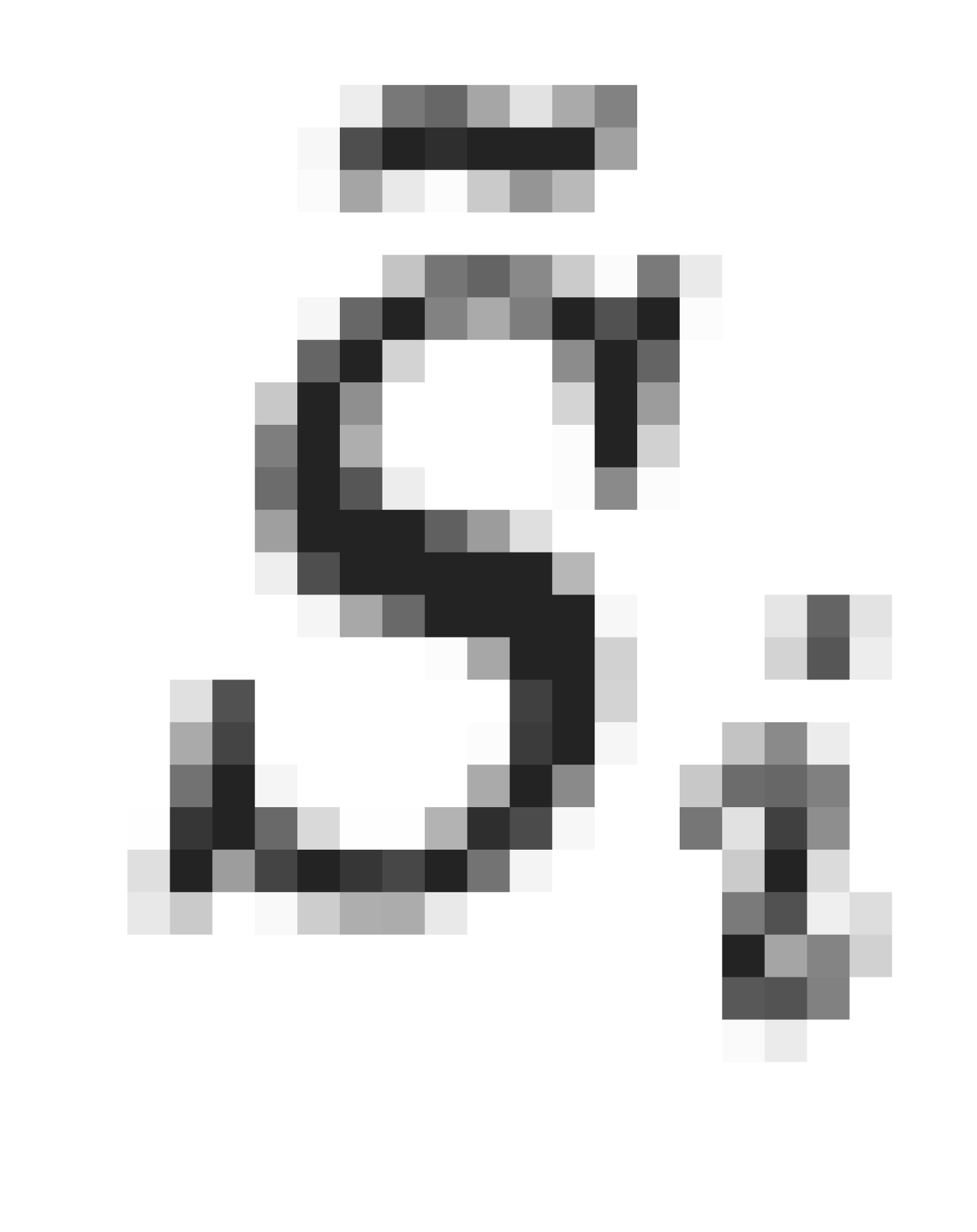คือ:

$$\begin{array}{r}\sum _{k=1}^N{({\tilde{S}}_k-{\tilde{S}}_{k-1})}^2=N\times {\left(\sqrt{\frac{T}{N}}\right)}^2=T\end{array}$$

ดังนั้น โดยการสร้างขึ้นมา ค่าการเปลี่ยนแปลงกำลังสองของการโยนเหรียญที่ถูกแก้ไข

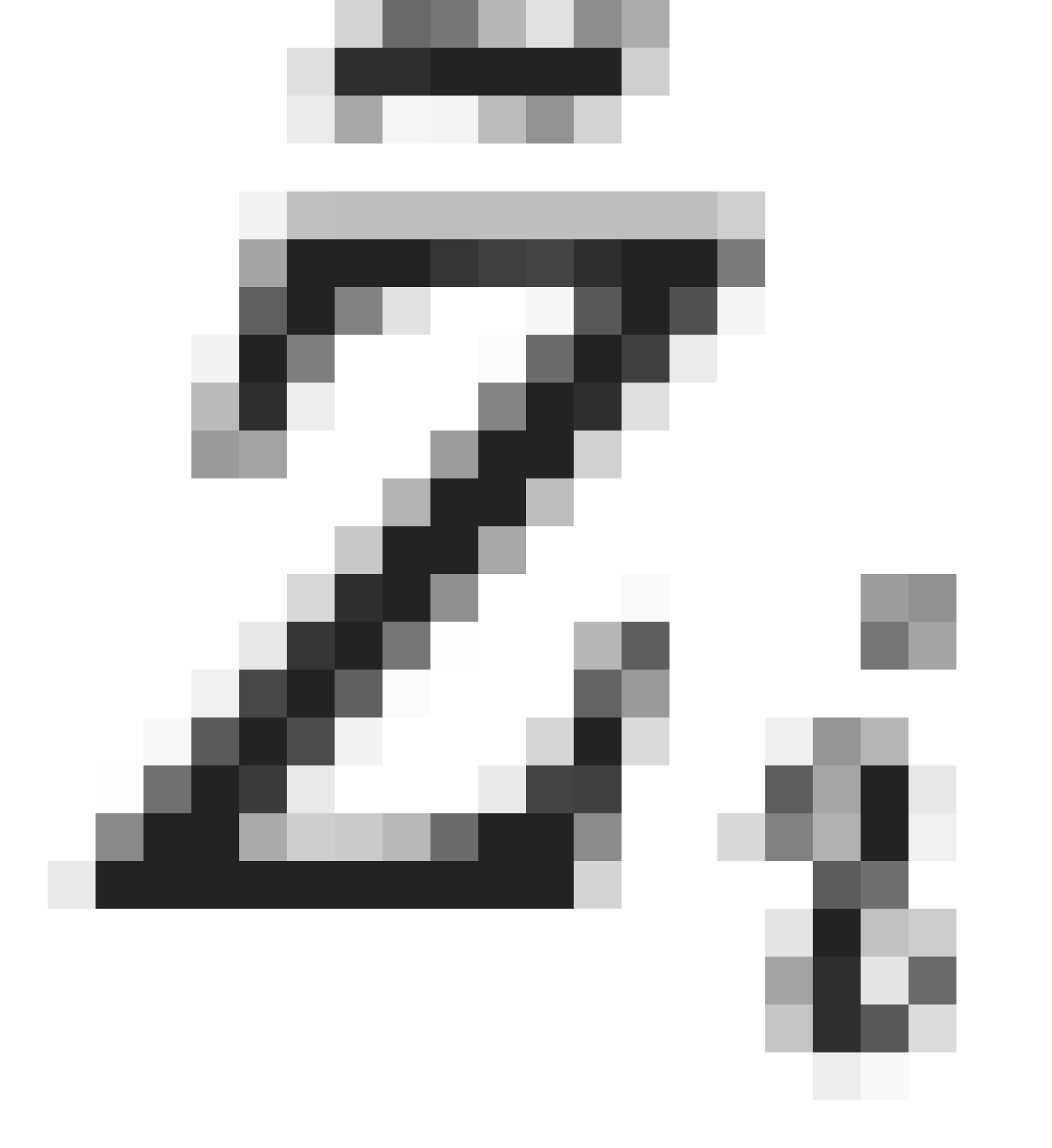   จะเท่ากับระยะเวลารวมของการโยนทั้งหมดคือ T

ที่สำคัญคือ ต้องสังเกตว่าคุณสมบัติของ Markov และ Martingale ยังคงอยู่ใน 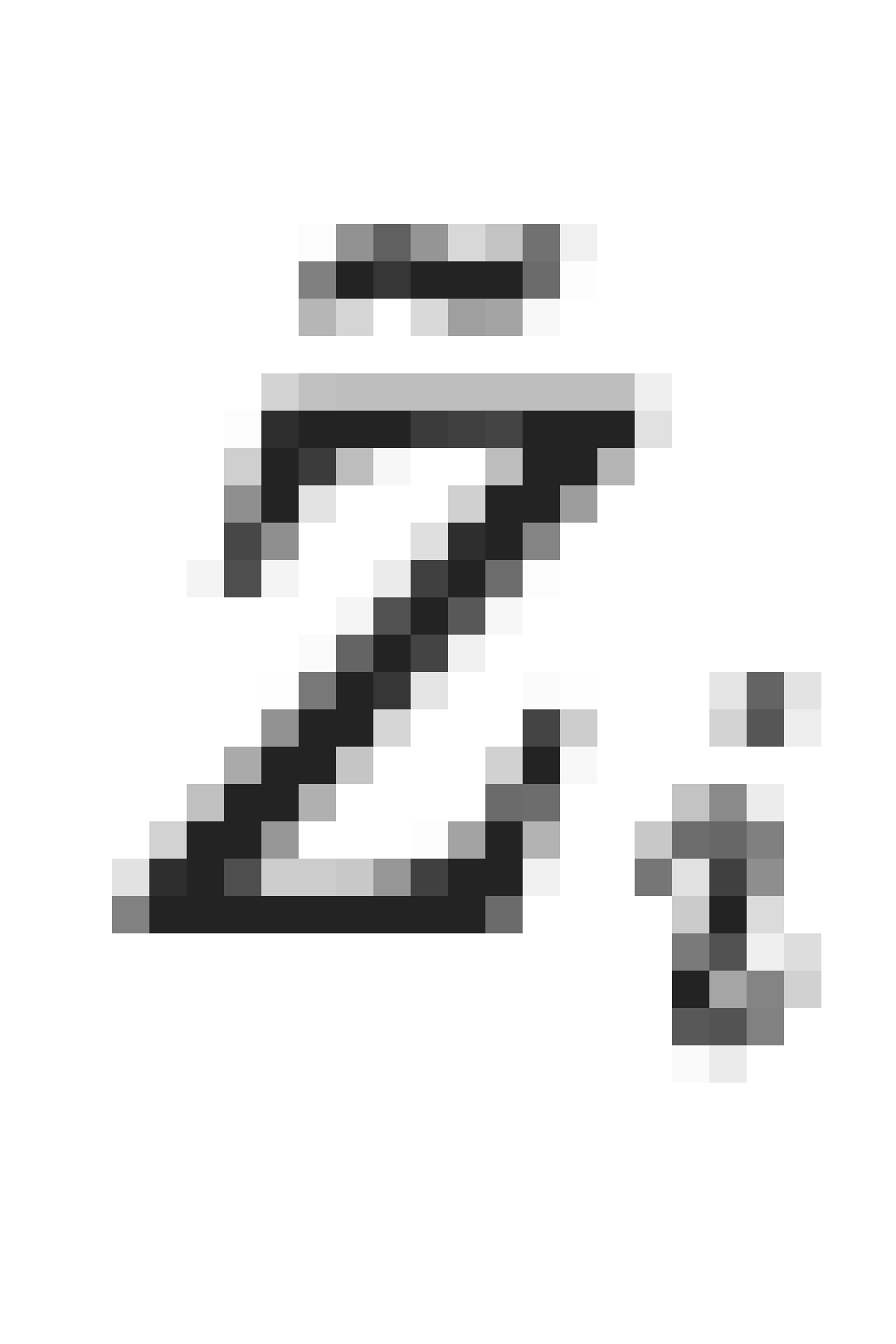 เมื่อ  การเดินสุ่มจากการโยนเหรียญจะไม่แยกออกจากกัน (ไม่ลู่ออกไปหรือ diverge) หากค่าของสินทรัพย์ในเวลา t โดยที่ 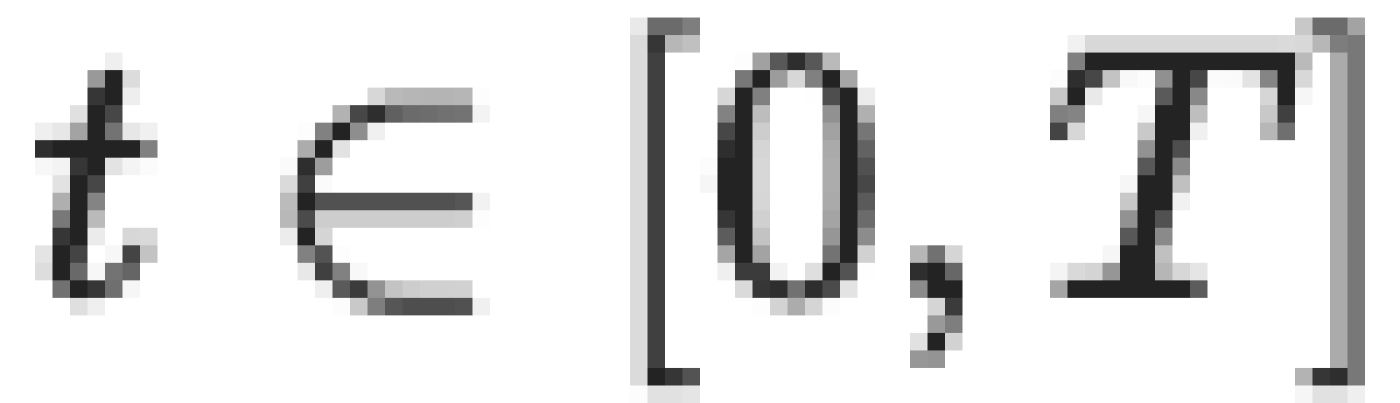 ถูกกำหนดให้เป็น S(t) ค่าคาดหมายแบบมีเงื่อนไขเมื่อสิ้นสุดช่วงเวลา โดยทราบว่า  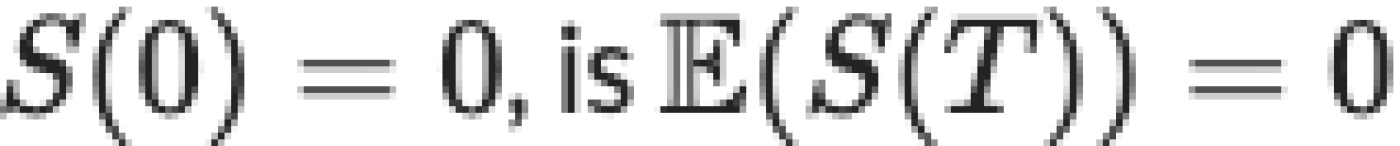และมีความแปรปรวนเท่ากับ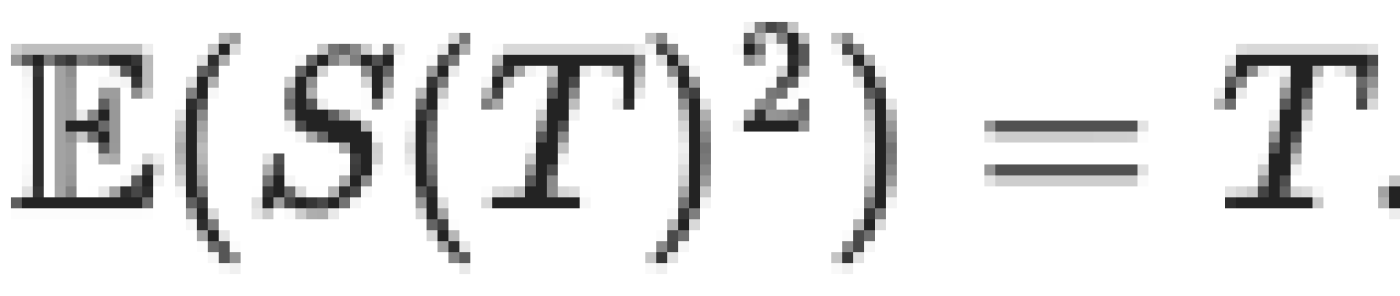 

แม้จะไม่กล่าวถึงรายละเอียดทางเทคนิค แต่เมื่อจำนวนขั้น N เข้าใกล้อินฟินิตี้ จะได้ Wiener process ซึ่งมักเรียกว่า standard Brownian motion และจะเขียนแทนด้วย B(t) โดยมีนิยามทางการดังนี้:

นิยาม: Wiener Process / Standard Brownian Motion

ลำดับของตัวแปรสุ่ม B(t) คือ Brownian motion ถ้า B(0) = 0 และสำหรับทุก t, s ที่ s < t จะมี B(t) - B(s) แจกแจงแบบปกติ (normally distributed) โดยมีความแปรปรวน t - s และการแจกแจงของ B(t) - B(s) ไม่ขึ้นอยู่กับ B(r) สำหรับ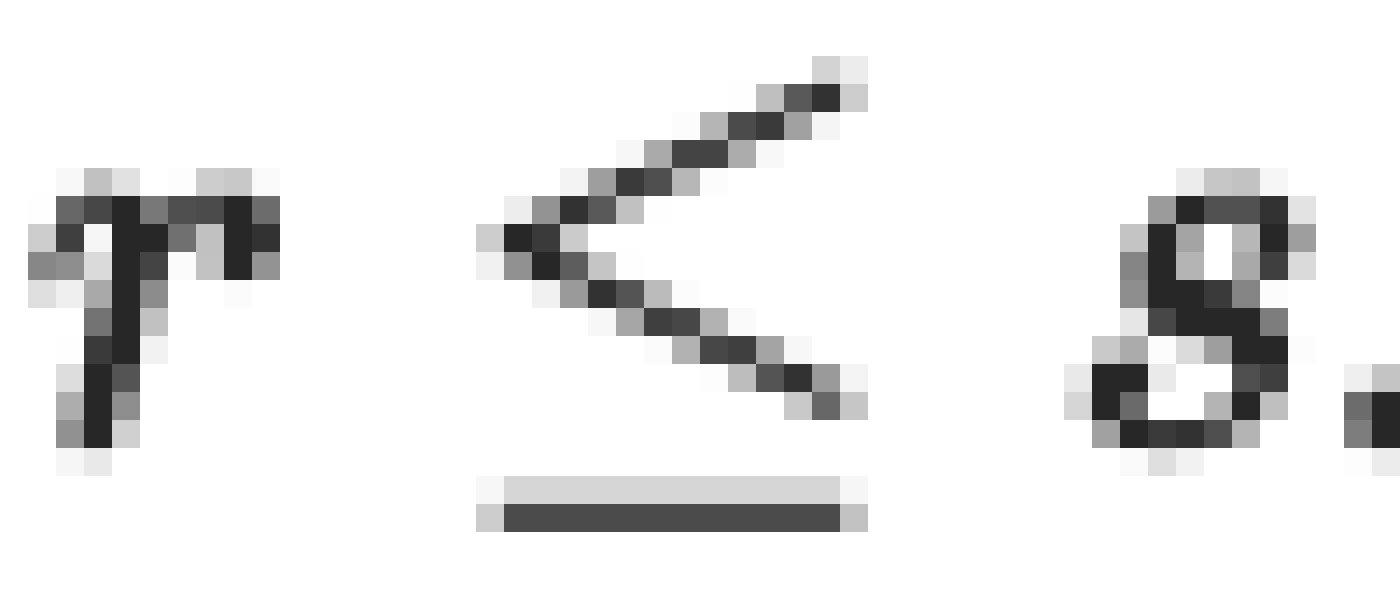 

คุณสมบัติของ Brownian Motion

Standard Brownian motion มีคุณสมบัติน่าสนใจหลายประการ ได้แก่:

• Brownian motions มีค่าจำกัด (finite): การสร้าง 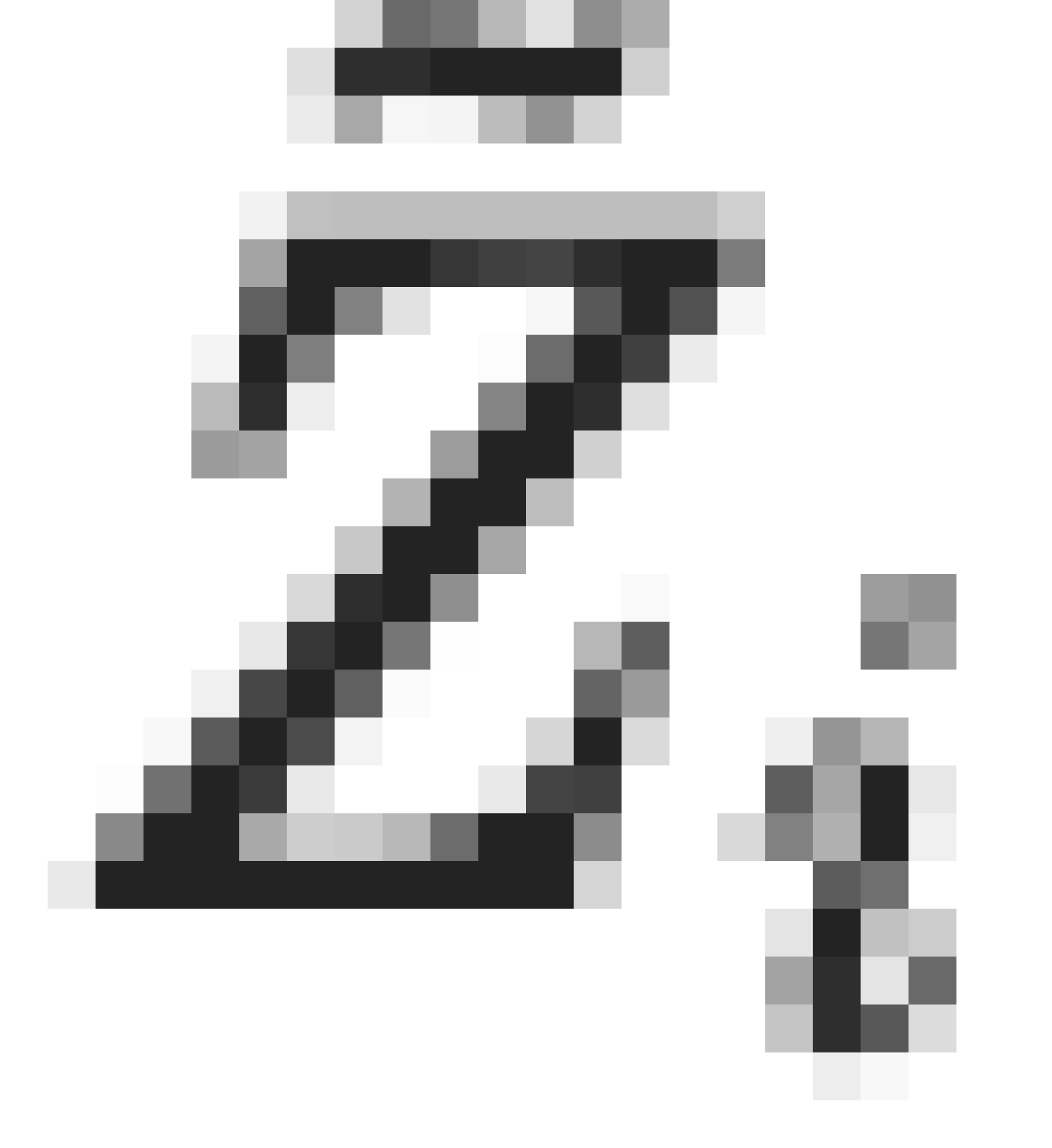 ถูกออกแบบมาอย่างระมัดระวังเพื่อให้เมื่อ N มีค่ามาก B ยังคงมีค่าจำกัดและไม่เป็นศูนย์

• Brownian motions มีการเปลี่ยนแปลงไม่จำกัด (unbounded variation): หมายความว่า ถ้าสลับสัญญาณของความชันลบทั้งหมดให้เป็นบวก B จะมีค่าเพิ่มขึ้นจนถึงอินฟินิตี้ภายในช่วงเวลาสั้นๆ ได้

• Brownian motions ต่อเนื่อง (continuous): แม้จะต่อเนื่องทุกจุด แต่จะไม่สามารถหาอนุพันธ์ได้ที่ใดเลย ซึ่งหมายความว่า Brownian motion มีเรขาคณิตแบบแฟร็กทัล (fractal geometry) ซึ่งมีผลสำคัญต่อวิธีการแคลคูลัสที่เลือกใช้เมื่อต้องวิเคราะห์หรือจัดการกับ Brownian motion

• Brownian motions สอดคล้องกับทั้งคุณสมบัติของ Markov และ Martingale: การแจกแจงแบบมีเงื่อนไขของ B(t) เมื่อทราบข้อมูลถึง s ขึ้นอยู่กับ t - s เท่านั้น และเมื่อทราบข้อมูลถึง s ค่าคาดหมายแบบมีเงื่อนไขของ B(t) คือ B(s)

• Brownian motions มีการแจกแจงแบบปกติอย่างเข้มข้น (strongly normally distributed): หมายความว่า สำหรับ t > s ค่าของ B(t) - B(s) แจกแจงแบบปกติโดยมีค่าเฉลี่ยเป็นศูนย์และความแปรปรวนเป็น t - s

โปรดทราบ: คุณสมบัติล่าสุดนี้ ไม่เหมือนกับ การที่ B(t) แจกแจงแบบปกติที่มีค่าเฉลี่ยเป็นศูนย์และความแปรปรวนเป็น t ซึ่งเป็นคุณสมบัติที่อ่อนกว่ามาก

Brownian motion เป็นองค์ประกอบพื้นฐานในการสร้างสมการเชิงอนุพันธ์สุ่ม (stochastic differential equations) ซึ่งในที่สุดจะนำไปสู่การหา สมการ Black-Scholes ที่มีชื่อเสียง สำหรับการกำหนดราคาของตราสารอนุพันธ์ (contingent claims)

อ้างอิง : Brownian Motion and the Wiener Process

จาก https://www.quantstart.com/articles/Brownian-Motion-and-the-Wiener-Process/