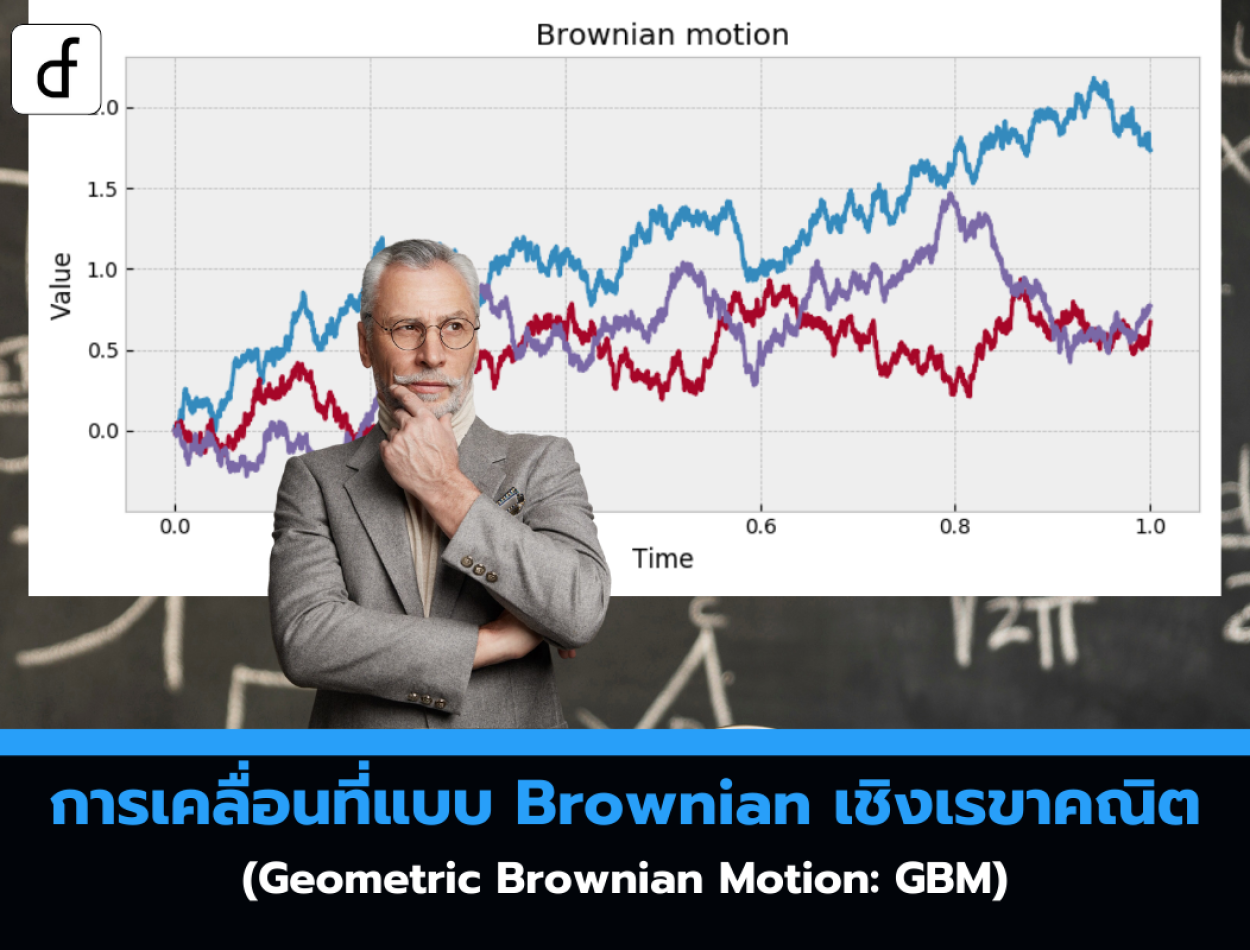
การเคลื่อนที่แบบ Brownian เชิงเรขาคณิต (Geometric Brownian Motion: GBM)

โมเดลปกติสำหรับการพัฒนาของราคาสินทรัพย์ S(t) คือการเคลื่อนที่แบบบราวเนียนเชิงเรขาคณิต ซึ่งแสดงโดยสมการอนุพันธ์สุ่มดังต่อไปนี้:

$$\begin{array}{r}dS(t)=\mu S(t)dt+\sigma S(t)dB(t)\end{array}$$

โปรดสังเกตว่าอัตราส่วน $\mu$ และ $\sigma$ ซึ่งแทนการลอยตัวและความผันผวนของสินทรัพย์ตามลำดับนั้นเป็นค่าคงที่ในโมเดลนี้ ในโมเดลที่ซับซ้อนกว่านี้ พวกมันสามารถถูกทำให้เป็นฟังก์ชันของ t, S(t) และกระบวนการสุ่มอื่น ๆ ได้

วิธีการหาคำตอบ S(t) สามารถทำได้โดยการใช้เกณฑ์ของอิโตะกับสมการอนุพันธ์สุ่ม

การหารด้วย S(t) ในสมการข้างต้นจะนำไปสู่:

$$\begin{array}{r}\frac{dS(t)}{S(t)}=\mu dt+\sigma dB(t)\end{array}$$

สังเกตว่าฝั่งซ้ายของสมการนี้ดูคล้ายกับอนุพันธ์ของ log S(t) การใช้กฎของอิโตะกับ log S(t) จะได้ว่า:

$$\begin{array}{r}d(logS(t))=(logS(t){)}^{\prime }\mu S(t)dt+(logS(t){)}^{\prime }\sigma S(t)dB(t)+\frac{1}{2}(logS(t){)}^{″}{\sigma }^{2}S(t{)}^{2}dt\end{array}$$

กลายเป็น:

$$\begin{array}{r}d(logS(t))=\mu dt+\sigma dB(t)-\frac{1}{2}{\sigma }^{2}dt=(\mu -\frac{1}{2}{\sigma }^2)dt+\sigma dB(t)\end{array}$$

นี่คือกระบวนการการแพร่กระจายแบบอิโตะ มันเป็นการเคลื่อนที่แบบบราวน์มาตรฐานที่มีเทอมการเลื่อน เนื่องจากสูตรข้างต้นเป็นเพียงการย่อส่วนของสูตรปริพันธ์ เราสามารถเขียนเป็นดังนี้:

$$\begin{array}{r}log(S(t))-log(S(0))=(\mu -\frac{1}{2}{\sigma }^2)t+\sigma B(t)\end{array}$$

สุดท้าย การนำเลขยกกำลังของสมการนี้จะให้:

$$\begin{array}{r}S(t)=S(0)\exp ((\mu -\frac{1}{2}{\sigma }^2)t+\sigma B(t))\end{array}$$

นี่คือวิธีแก้สมการอนุพันธ์สุ่ม ในความเป็นจริง นี่เป็นหนึ่งในไม่กี่วิธีการวิเคราะห์ที่สามารถหาได้จากสมการอนุพันธ์สุ่ม

อ้างอิง: Geometric Brownian Motion

จาก https://www.quantstart.com/articles/Geometric-Brownian-Motion/